Description cinétique

Pour décrire un plasma ou un gaz, on peut soit utiliser les méthodes de l'hydrodynamique en considérant des grandeurs macroscopiques telles que la densité ou la vitesse du fluide, soit tenir compte de la nature moléculaire du fluide à partir des fonctions de distribution des vitesses qui donnent une description microscopique classique du fluide. Dans cette partie, nous allons donner les relations existant entre les grandeurs macroscopiques et les fonctions de distribution.

Dans une description statistique, le nombre probable de particules dans un élément de volume à 6 dimensions (3 dimensions de position, 3 dimensions de vitesse ou de quantité de mouvement) est $f(\vec r, \vec v, t) d\vec{r} d\vec{v}$ où $f(\vec r, \vec v, t)$ s'appelle la fonction de distribution de cette population de particules. Une équation cinétique est une équation qui permet de déterminer la fonction de distribution en tenant compte des forces microscopiques dues aux collisions et des forces macroscopiques telles que les champs appliqués :

$$\frac{\partial f}{\partial t} + \vec v \cdot \frac{\partial ... ...ial \vec v} = \left( \frac{\partial f}{\partial t} \right)_{c}$$ (II.A.1)

où $\vec F$ contient les forces macroscopiques ainsi que le champ électrique moyen dû aux particules donné de façon auto-consistante par l'équation de Poisson

$$div(\vec E) = \frac{1}{\epsilon_{0}} \sum_{i} q_{i} \int f_{i}(\vec r, \vec v, t) d\vec v ,$$

et éventuellement un champ magnétique $\vec B$ donné par

$$\vec{rot}(\vec B) = \mu_{0} \sum_{i} q_{i} \int f_{i}(\vec r, \vec v, t) \vec v d\vec v ,$$

et le second membre rend compte des collisions entre particules.

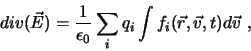
Pour obtenir les grandeurs macroscopiques, on calcul les différents moments de la fonction de distribution :

• la densité de particules
  

  $$n(\vec r, t) = \int f(\vec r, \vec v, t) d\vec v ;$$ (II.A.2)

  
  

• la vitesse moyenne des particules
  

  $$\vec u(\vec r, t) = \frac{\int \vec v f(\vec r, \vec v, t) d... ...ac{1}{n(\vec r, t)} \int \vec v f(\vec r, \vec v, t) d\vec v ;$$ (II.A.3)

  
  

• l'énergie cinétique moyenne
  

  $$\overline{E_{c}} = \frac{1}{n} \int \frac{1}{2} m \vec v^{2} d\vec v ;$$ (II.A.4)

  
  

• le tenseur de pression cinétique
  

  $$\overline{\overline{P}}(\vec r, t) = m \int (\vec v - \vec u)\otimes (\vec v - \vec u) f(\vec r, \vec v, t) d\vec v$$ (II.A.5)

  
  
  où $\otimes$ représente le produit tensoriel ;

• le flux d'énergie thermique
  

  $$\overline{\overline{\overline{Q}}}(\vec r, t) = m \int (\vec... ...vec u)\otimes (\vec v - \vec u) f(\vec r, \vec v, t) d\vec v .$$ (II.A.6)

  
  

À partir de l'équation II.1 de la fonction de distribution, on peut écrire les équations de conservation de la masse, de la quantité de mouvement et de l'énergie des grandeurs macroscopiques. Par conséquent, en théorie la détermination de la fonction de distribution permet de déduire toutes les grandeurs macroscopiques du fluide.