Équations de dispersion

Afin d'écrire les relations de dispersion, nous devons définir les conditions aux limites et les conditions de continuité des paramètres du plasma pour le modèle de joa93.

Les conditions de continuité sont définies aux interfaces entre le milieu intérieur et le milieu extérieur : continuité de la composante $v_{x}$ et de la pression totale $p$ en $\pm a$. Ces conditions imposent la continuité des perturbations de vitesse $\delta \vec v$, de pression $\delta p$ et de champ magnétique $\delta B_{y}$ et $\delta B_{z}$ en $\pm a$.

Les conditions aux limites sont imposées par les murs parfaitement conducteurs situés dans le milieu extérieur en $\pm l$ : les composantes de la vitesse $\delta \vec v$ sont nulles en $\pm l$.

Par conséquent, le système à résoudre se réduit à un système linéaire à 18 inconnues. Pour obtenir les équations de dispersion, nous allons réduire le système aux seuls modes d'Alfvén que l'on peut facilement découpler des modes magnétoacoustiques. Le système linéaire est de la forme $M\alpha = 0$ avec $\alpha$ un vecteur à six éléments contenant les constantes déjà mentionnées dans la section précédente et M la matrice suivante (l'indice "o" représente le milieu intérieur et "e" le milieu extérieur) :

$$\left( \begin{array}{c c c c c c} 0 & 0 & -k_{ao}e^{-ik_{ao}... ...-e^{ik_{ao}a} & -e^{-ik_{ao}a} & 0 & 0 \\ \end{array} \right)$$

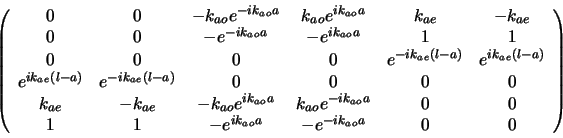
Le système posséde des solutions non-triviales uniquement si le déterminant de la matrice M est nul, c'est-à-dire :

$$(k_{ae} - k_{ao})(e^{2i(k_{ae} + k_{ao})a} + e^{2ik_{ae}l}) ... ...{ao})(e^{2i(k_{ae} + k_{ao})a} + e^{2ik_{ae}l}) = 0 \nonumber$$

On obtient alors les deux relations de dispersion pour le mode d'Alfvén pair :

$$\tan{(\frac{w a}{v_{Axo}})} - \sqrt{\frac{\rho_{e}}{\rho_{o}}} \cot{(\frac{w (l - a)}{v_{Axe}})} = 0,$$ (V.A.12)

et pour le mode d'Alfvén impair :

$$\cot{(\frac{w a}{v_{Axo}})} + \sqrt{\frac{\rho_{e}}{\rho_{o}}} \cot{(\frac{w (l - a)}{v_{Axe}})} = 0.$$ (V.A.13)

En suivant la même méthode, nous obtenons les équations de dispersion pour les modes magnétoacoustiques :

$$\tan{(\frac{w a}{c^{+}_{o}})} - \sqrt{\frac{\rho_{e}}{\rho_{o}}} \cot{(\frac{w (l - a)}{c^{+}_{e}})} = 0$$ (V.A.14)

pour le mode magnétoacoustique lent "kink",

$$\cot{(\frac{w a}{c^{+}_{o}})} + \sqrt{\frac{\rho_{e}}{\rho_{o}}} \cot{(\frac{w (l - a)}{c^{+}_{e}})} = 0$$ (V.A.15)

pour le mode magnétoacoustique lent "sausage",

$$\tan{(\frac{w a}{c^{-}_{o}})} - \sqrt{\frac{\rho_{e}}{\rho_{o}}} \cot{(\frac{w (l - a)}{c^{-}_{e}})} = 0$$ (V.A.16)

et pour le mode magnétoacoustique rapide "kink",

$$\cot{(\frac{w a}{c^{-}_{o}})} + \sqrt{\frac{\rho_{e}}{\rho_{o}}} \cot{(\frac{w (l - a)}{c^{-}_{e}})} = 0$$ (V.A.17)

pour le mode magnétoacoustique rapide "sausage".

Ces relations de dispersion fournissent des spectres de fréquences discrétisés et non-équidistants.