



suivant: Loi d'Ohm, MHD idéale
monter: La MHD
précédent: Équations de Maxwell
Table des matières
Les mouvements d'un plasma de densité  sont gouvernés par
des équations de conservation de la masse, de la quantité de mouvement ou
l'énergie. Ces relations sont déduites des différents moments de la
fonction de distribution associée au plasma et considérée comme une
distribution maxwellienne.
sont gouvernés par
des équations de conservation de la masse, de la quantité de mouvement ou
l'énergie. Ces relations sont déduites des différents moments de la
fonction de distribution associée au plasma et considérée comme une
distribution maxwellienne.
L'équation de continuité ou de conservation de la masse s'écrivant :
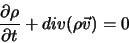 |
(II.B.14) |
traduit le fait que la masse est distribuée continuement dans le plasma.
Pour un plasma électriquement neutre soumis aux seules forces de pression, de
Lorentz, de gravité et de viscosité, l'équation du mouvement (ou conservation de la
quantité de mouvement) s'écrit :
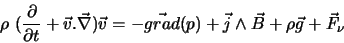 |
(II.B.15) |
où p représente le champ de pression cinétique,  est le champ de
gravité. La force de viscosité s'écrit
est le champ de
gravité. La force de viscosité s'écrit
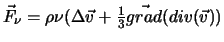 où
où  est le coefficient de
viscosité cinématique.
est le coefficient de
viscosité cinématique.
Suivant les mêmes hyphothèses (en négligeant la viscosité),
l'équation de conservation de l'énergie cinétique s'écrit :
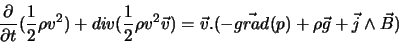 |
(II.B.16) |
et l'équation de conservation de l'énergie interne U est
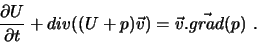 |
(II.B.17) |
Comme nous avons négligé ici la viscosité et les sources ou pertes de
chaleur, nous nous
situons dans l'hypothèse adiabatique qui nous permet de réécrire
l'équation précédente sous la forme
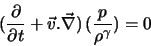 |
(II.B.18) |
où 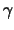 est le coefficient adiabatique (rapport des chaleurs
spécifiques
est le coefficient adiabatique (rapport des chaleurs
spécifiques 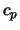 et
et 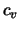 ). L'équation de conservation de l'énergie
totale est alors la somme des équations II.16 et II.18 : conservation de
l'énergie cinétique et de l'énergie interne.
). L'équation de conservation de l'énergie
totale est alors la somme des équations II.16 et II.18 : conservation de
l'énergie cinétique et de l'énergie interne.
D'autre part, la densité de charge 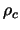 dans un plasma se conserve :
dans un plasma se conserve :
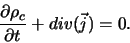 |
(II.B.19) |
Dans le cas d'un plasma électriquement neutre, la conservation de la
densité de charge se réduit à
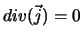




suivant: Loi d'Ohm, MHD idéale
monter: La MHD
précédent: Équations de Maxwell
Table des matières
Stephane Regnier
2002-03-29
![]() sont gouvernés par
des équations de conservation de la masse, de la quantité de mouvement ou
l'énergie. Ces relations sont déduites des différents moments de la
fonction de distribution associée au plasma et considérée comme une
distribution maxwellienne.
sont gouvernés par
des équations de conservation de la masse, de la quantité de mouvement ou
l'énergie. Ces relations sont déduites des différents moments de la
fonction de distribution associée au plasma et considérée comme une
distribution maxwellienne.
![]() dans un plasma se conserve :
dans un plasma se conserve :
![]()