



suivant: Hypothèses de la MHD
monter: La MHD
précédent: Équations de conservation
Table des matières
Loi d'Ohm, MHD idéale
La loi d'Ohm pour un conducteur en mouvement dans un champ magnétique est
donnée par :
 |
(II.B.20) |
où 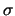 est la conductivité électrique du plasma. De cette équation
et des équations de Maxwell, nous en déduisons l'équation d'évolution
du champ magnétique :
est la conductivité électrique du plasma. De cette équation
et des équations de Maxwell, nous en déduisons l'équation d'évolution
du champ magnétique :
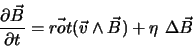 |
(II.B.21) |
avec
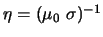 le coefficient de diffusion magnétique,
et où le premier terme du second membre est le terme de convection, et le second
terme est un terme de diffusion. Pour caractériser l'importance relative des
deux termes, on forme le nombre sans dimension appelé le nombre de Reynolds
magnétique :
le coefficient de diffusion magnétique,
et où le premier terme du second membre est le terme de convection, et le second
terme est un terme de diffusion. Pour caractériser l'importance relative des
deux termes, on forme le nombre sans dimension appelé le nombre de Reynolds
magnétique :
![\begin{displaymath}
R_{B} = \frac{v l}{\eta} = \left[ \frac{convection}{diffusion} \right]
\end{displaymath}](img123.gif) |
(II.B.22) |
avec 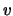 la vitesse et
la vitesse et 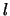 la longueur caractérisant l'écoulement.
Pour
la longueur caractérisant l'écoulement.
Pour  dans lequel la convection domine, on suppose généralement
que la conductivité électrique
dans lequel la convection domine, on suppose généralement
que la conductivité électrique 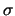 devient infinie. La loi d'Ohm
implique alors que :
devient infinie. La loi d'Ohm
implique alors que :
 |
(II.B.23) |
On se place alors dans le cadre de la MHD idéale. Les équations
II.21 et II.23 ont pour conséquence le théorème du
gel : les lignes de champ magnétique évoluent avec le plasma. Dans le cadre
de la MHD idéale, il existe un certain
nombre de paramètres se conservant tels que le moment magnétique orbital
 ou encore l'hélicité magnétique
ou encore l'hélicité magnétique  . Cette dernière
quantité donnée par :
. Cette dernière
quantité donnée par :
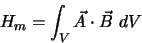 |
(II.B.24) |
rend compte des propriétés topologiques du champ magnétique (cf revue de
ber99). Par contre, cette expression de l'hélicité est sensible
à la condition de jauge imposée (condition de fermeture imposée au
potentiel vecteur). Pour pallier cette condition, ber84 ont défini
l'hélicité magnétique relative  dans un volume
dans un volume 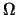 en
faisant intervenir le champ potentiel
en
faisant intervenir le champ potentiel  (
(
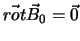 ) avec les mêmes conditions
aux limites imposées au champ
) avec les mêmes conditions
aux limites imposées au champ 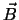 :
:
 |
(II.B.25) |
où  (resp.
(resp. 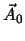 ) est le potentiel vecteur associé au champ
magnétique
) est le potentiel vecteur associé au champ
magnétique 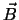 (resp.
(resp.  ),
), 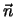 est la normale à la surface.
est la normale à la surface.
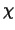 s'exprime à partir de
s'exprime à partir de 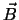 et de
et de  (ber84). On
peut considérer deux cas particuliers :
(ber84). On
peut considérer deux cas particuliers :
- si le volume
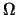 est un demi-espace, l'intégrale de surface tend
alors vers zéro ;
est un demi-espace, l'intégrale de surface tend
alors vers zéro ;
- si on impose que la composante normale du champ magnétique doit être
nulle à la surface limitant le volume
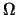 , alors l'intégrale de
surface est exactement égale à zéro.
, alors l'intégrale de
surface est exactement égale à zéro.
Ces deux cas conduisent à l'expression de l'hélicité magnétique
relative suivante :
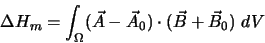 |
(II.B.26) |




suivant: Hypothèses de la MHD
monter: La MHD
précédent: Équations de conservation
Table des matières
Stephane Regnier
2002-03-29