| (V.C.3) |
Pour déterminer les modes d'oscillation du filament, nous linéarisons les
équations de la MHD (cf Chap. II) en introduisant des
perturbations de déplacement, de vitesse, de champ magnétique, de pression
et de densité de la forme :
| (V.C.3) |
où ![]() est la fréquence de la perturbation, et
est la fréquence de la perturbation, et ![]() ,
, ![]() ,
,
![]() les nombres d'onde dans chaque direction. L'ensemble des calculs
permettant l'obtention des relations de dispersion des ondes pouvant exister
dans ce modèle est détaillé dans l'annexe V.A. Les principales
hypothèses de ce modèle sont de considérer que
les nombres d'onde dans chaque direction. L'ensemble des calculs
permettant l'obtention des relations de dispersion des ondes pouvant exister
dans ce modèle est détaillé dans l'annexe V.A. Les principales
hypothèses de ce modèle sont de considérer que ![]() , et que l'on
se situe dans l'approximation des grandes longueurs d'onde, c'est-à-dire que
, et que l'on
se situe dans l'approximation des grandes longueurs d'onde, c'est-à-dire que
![]() . Les conditions aux limites sont fixées par l'effet des
murs rigides en
. Les conditions aux limites sont fixées par l'effet des
murs rigides en ![]() :
:
![]() . Les
conditions de continuité sont déterminées à l'interface entre le milieu
intérieur et le milieu extérieur : continuité de la pression totale et de
la composante
. Les
conditions de continuité sont déterminées à l'interface entre le milieu
intérieur et le milieu extérieur : continuité de la pression totale et de
la composante ![]() de la vitesse en
de la vitesse en ![]() . Ces conditions
conduisent à la continuité de
. Ces conditions
conduisent à la continuité de ![]() ,
, ![]() ,
, ![]() et de
et de ![]() . Les six modes obtenus sont les modes d'Alfvén pair et
impair avec une vitesse caractéristique
. Les six modes obtenus sont les modes d'Alfvén pair et
impair avec une vitesse caractéristique ![]() (vitesse d'Alfvén suivant
l'axe x), les modes magnétoacoustiques (lents et rapides) "sausage" et "kink"
de vitesses caractéristiques
(vitesse d'Alfvén suivant
l'axe x), les modes magnétoacoustiques (lents et rapides) "sausage" et "kink"
de vitesses caractéristiques
![]() (
(![]() pour les modes lents,
pour les modes lents,
![]() pour les modes rapides) où
pour les modes rapides) où ![]() est la vitesse du son dans le milieu
et
est la vitesse du son dans le milieu
et
![]() .
Ils satisfont aux équations de dispersion suivantes :
.
Ils satisfont aux équations de dispersion suivantes :
Ces équations de dispersion possèdent une infinité de solutions. La
fréquence
la plus basse est appelée la fréquence primaire, les suivantes étant les
fréquences secondaires. En supposant
que
![]() , on peut donner une forme approchée de la fréquence
primaire et des fréquences secondaires de modes (Tab. V.2). Nous
nous sommes restreints aux fréquences inférieures à 6 mHz (périodes
supérieures à
, on peut donner une forme approchée de la fréquence
primaire et des fréquences secondaires de modes (Tab. V.2). Nous
nous sommes restreints aux fréquences inférieures à 6 mHz (périodes
supérieures à ![]() 3 min). Les
fréquences secondaires ne sont pas des fréquences
harmoniques de la fréquence principale du mode considéré. On notera aussi
que les fréquences secondaires peuvent se scinder en deux sous-catégories :
les fréquences des modes internes (ne dépendant que de la vitesse du milieu
intérieur) et les fréquences des modes externes (ne dépendant que de la
vitesse du milieu extérieur).
3 min). Les
fréquences secondaires ne sont pas des fréquences
harmoniques de la fréquence principale du mode considéré. On notera aussi
que les fréquences secondaires peuvent se scinder en deux sous-catégories :
les fréquences des modes internes (ne dépendant que de la vitesse du milieu
intérieur) et les fréquences des modes externes (ne dépendant que de la
vitesse du milieu extérieur).
Par la suite, nous utiliserons la notation suivante : "eAm" pour le mode
d'Alfvén pair, "oAm" pour le mode d'Alfvén impair, "skm" pour le
mode lent "kink", "ssm" pour le mode lent "sausage", "fkm" pour le
mode rapide "kink" et "fsm" pour le mode rapide "sausage" ; les
fréquences des modes secondaires internes (externes) sont notées
![]() (
(![]() ) avec
) avec ![]() .
.
À partir du tableau V.2, nous avons calculé les rapports des
fréquences primaires et des fréquences secondaires :
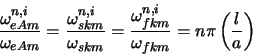 |
(V.C.7) |
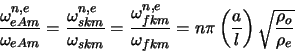 |
(V.C.8) |
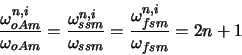 |
(V.C.9) |
 |
(V.C.10) |
Il est intéressant de remarquer que le rapport des fréquences primaires,
Éq.(V.6), ne dépend que des caractéristiques géométriques du
modèle, ![]() et
et ![]() , et par conséquent ne dépend ni de l'angle
, et par conséquent ne dépend ni de l'angle ![]() , ni
de la densité, ni de la température et ni du champ magnétique. Ce rapport
est noté
, ni
de la densité, ni de la température et ni du champ magnétique. Ce rapport
est noté ![]() :
:
![]() est le rapport de la fréquence primaire d'un mode pair sur la
fréquence primaire du mode impair associé. Comme le modèle suppose que
est le rapport de la fréquence primaire d'un mode pair sur la
fréquence primaire du mode impair associé. Comme le modèle suppose que
![]() ,
, ![]() est toujours inférieur à 1. Par conséquent, la
fréquence primaire du mode pair est toujours plus petite que la fréquence
primaire du mode impair associé.
est toujours inférieur à 1. Par conséquent, la
fréquence primaire du mode pair est toujours plus petite que la fréquence
primaire du mode impair associé.