| (II.C.31) |
Pour une densité de courant différente de zéro dans tout le volume
contenant le plasma, l'équation II.28 signifie que le vecteur
champ magnétique et le vecteur densité de courant sont parallèles. Par
conséquent, l'équation II.12 s'écrit :
Le champ magnétique vérifiant les équations II.31 et
II.32 est appelé champ sans-force. Si ![]() a la même valeur
pour chaque ligne de champ, alors nous obtenons le cas sans-force linéaire ou
à
a la même valeur
pour chaque ligne de champ, alors nous obtenons le cas sans-force linéaire ou
à ![]() constant pour lequel l'équation II.31 devient
constant pour lequel l'équation II.31 devient
| (II.C.33) |
Malgré les difficultés à résoudre les équations du champ sans-force,
on peut en déduire des relations intéressantes. En particulier,
mol69 a mis en évidence des propriétés intégrales du champ
sans-force :
 |
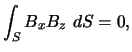 |
||
 |
 |
(II.C.34) | |
 |
 |
| (II.C.35) |
L'hélicité magnétique (Sect. 2.3) possède aussi des caractéristiques
particulières dans le cas d'un champ sans-force.
wol58 a démontré que, pour un plasma parfaitement conducteur,
l'hélicité magnétique dans un volume fermé V![]() est invariante et
que l'état de minimum d'énergie correspond à un champ sans-force
linéaire. tay74 a étendu les travaux de wol58 : pour un
plasma parfaitement conducteur, l'hélicité magnétique est invariante pour
chaque tube de flux, et le minimum d'énergie est obtenu pour un champ
sans-force linéaire. tay74 a aussi suggéré que, pour un plasma
avec une faible résistivité, les modifications dans la topologie de la
configuration magnétique étaient accompagnées par de faibles changements
du champ magnétique, mais que globalement l'hélicité magnétique dans le
volume total était inchangée.
Par conséquent, l'hélicité est approximativement invariante et, d'après
wol58, le minimum
d'énergie est obtenu pour le champ sans-force linéaire : c'est
l'hypothèse de tay74.
est invariante et
que l'état de minimum d'énergie correspond à un champ sans-force
linéaire. tay74 a étendu les travaux de wol58 : pour un
plasma parfaitement conducteur, l'hélicité magnétique est invariante pour
chaque tube de flux, et le minimum d'énergie est obtenu pour un champ
sans-force linéaire. tay74 a aussi suggéré que, pour un plasma
avec une faible résistivité, les modifications dans la topologie de la
configuration magnétique étaient accompagnées par de faibles changements
du champ magnétique, mais que globalement l'hélicité magnétique dans le
volume total était inchangée.
Par conséquent, l'hélicité est approximativement invariante et, d'après
wol58, le minimum
d'énergie est obtenu pour le champ sans-force linéaire : c'est
l'hypothèse de tay74.